a

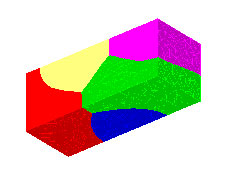
Initial (t=0) microstructure for a  short metallic line used in the gradient-weighted finite element calculations (b) and (c), generated by discrete Potts evolution of random effective spins on the elements of the tetrahedral LaGriT mesh followed by a few timesteps of evolution under mean curvature to remove discrete artifacts.

b

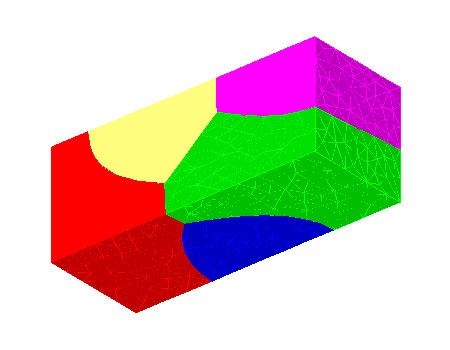
Microstructure at t=4 using mean curvature grain boundary motion.

c

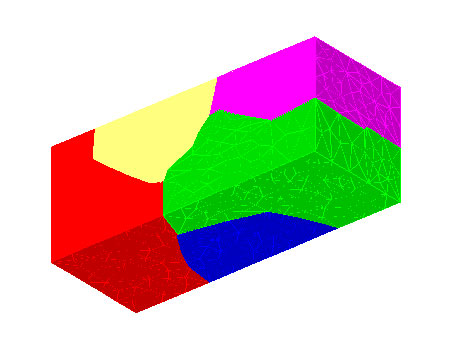
Microstructure at t=4 when an orientation dependent grain boundary energy is used. Note that while the gross features of (b) and (c) are the same, the  mean curvature evolution in (b) accurately reproduces the well-known predictions for mean curvature motion (grains meeting at triple lines with 120 degree angles, etc), whereasthe orientation dependent grainboundary energy used in (c) gives rise to the steps and facets expected for crytalline metals such as Copper.

d

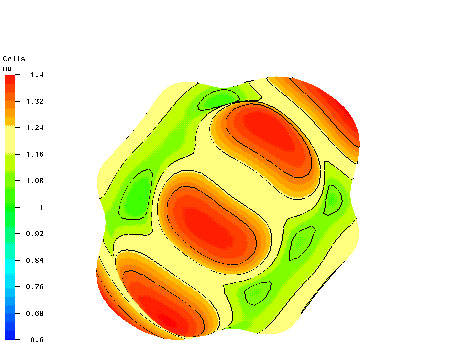
Orientation-dependence of the grain boundary energy between grains 3 and 4 of Figure 1. The figure has the same orientation as Figure 1. The direction to the surface from the center is the direction of the grain boundary normal, and the length of the vector (and color of the surface) gives the magnitude.  This surface is different for each grain pair since it is a function of their relative orientations as well as the grain boundary normal dependence shown here. The interactionwith the boundary for this simulation was chosen to be grain and orientation independent. The grains have fcc symmetry and the parameters were chosen to approximate Copper. We are currently investigating ways to more accurately model the orientation dependence within the scope of the finite element calculation.