Releases a previously defined surface.
ibtype can be free, intrface, reflect, intrcons or virtual. Use reflect or free for external boundaries, intrface for interior interfaces, intrcons for constrained interior interfaces. Use virtual for virtual interfaces. Nodes on reflect, intrcons, or virtual interfaces will be assigned icrl values corresponding to the surfaces on which the nodes sit. The command settets will generate parent/child node chains (isn1) for nodes on intrface or intrcons. Surfaces which have different materials on either side of the surface virtual interfaces do not separate material regions but are intended to identify other structural features of a geometry. The surface is defined by a set of surface-parameters.
istype can be plane, box, parallel(piped), sphere, cylinder, cone, ellipse(oid), tabular (rotated tabular profile), or sheet. Surface-parameters are specified with the surface type in mind.
isurname is the name of the surface and must be unique for each surface defined by surface.
surface/isurname/ibtype/sheet/cmo-name
surface/isurname/release
Release the previously defined surface named s1. Remove all references from the geometry data structures and remove all constraints associated with this surface.
surface/sbox/ibtype/box/xmin,ymin,zmin/xmax,ymax,zmax/
Where xmin,ymin,zmin and xmax,ymax,zmax are the coordinates of opposite corners of a cube, i.e bottom left and top right corners.
surface/mysurf/ibtype/cone/x1,y1,z1/x2,y2,z2/radius/
Where point 1 is the vertex and point 2 is the top center of the cone with radius from that point. A cone is finite but open. To create a closed cone cap the open end with a plane.
surface/acyl/ibtype/cylinder/x1,y1,z1/x2,y2,z2/radius
Where point 1 is the bottom center and point 2 is the top center of the cylinder. radius is the radius of the cylinder. Cylinders are open but finite. To create a closed cylinder cap both ends with planes.
surface/sellip/ibtype/ellipse/x1,y1,z1/x2,y2,z2/x3,y3,z3/ar,br,cr/
Where point 1 is the center of the ellipsoid and point 2 is on the a semi-axis (new x), point 3 is on the b semi-axis (new y), and ar, br, cr are radii on their respective semi-axes.
surface/s2/ibtype/parallel/x1,y1,z1/x2,y2,z2/x3,y3,z3/x4,y4,z4/
Where points 1, 2, 3 are the front left, front right and back left points of the base and point 4 is the upper left point of the front face.
surface/s1/ibtype/plane/x1,y1,z1/x2,y2,z2/x3,y3,z3
surface/top/ibtype/planexyz/x1,y1,z1/x2, z2/x3,y3,z3
the direction of the normal to the plane is determined by the order of the points according to the right hand rule.
surface/bot/ibtype/planertz/radius1,theta1,z1,radius2,theta2,z2,radius ,zcen/
surface/s10/ibtype/planertp/radius1,theta1,p
surface/asheet/ibtype/sheet/cmo_name/<
Sheet surfaces may be input by specifying a cmo_name. The Mesh Object must be either a 2D quad Mesh Object or a 2D triangle Mesh Object. A discussion of inside and outside with respect to sheet surfaces is presented after the EXAMPLES section.
surface/sphere1/ibtype/sphere/x_center,y_center,z_center,radius
surface/s3/ibtype/tabular/x1,y1,z1/x2,y2,z2/rz|rt/&
r1,z1 &
r2,z2 &
r3,z3 &
....
rn,zn &
end
or
r1,theta1 &
r2,theta2 &
r3,theta3 &
...
rn,thetan &
end
Where point 1 and point 2 define the axis of rotation for the tabular profile with point 1 as the origin. This is followed by pairs of profile descriptors depending on the value of geom.Ifgeom is set to rz, then the r value is a radius normal to the axis of rotation and z is the distance along the new axis of rotation. If geomis set to rt then theta is the angle from the axis of rotation at point 1 andris the distance from point 1 along theta. The first pair must start on a new line and all lines must contain pairs of data. The last pair of data must be followed by end.
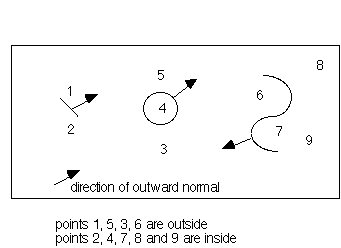
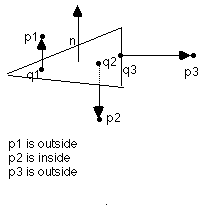
Inside/outside with respect to sheet surfaces will be determined by the following algorithm:
* Construct
the vector
, from q to p.
* Construct
the outward normal to the triangle, 
.
The outward normal is constructed using the right hand rule and the order
of the points in the sheet. Sheets may be specified as quad Mesh Object
(i.e. a 2 dimensional array of points containing the coordinates of the
corners of each quad). Either two triangles (divide each quad in two using
point (i,j) and (i+1,j+1)) or four triangles (add a point in the center
of the quad) are generated by each quad. Applying the right hand rule to
the points (i,j), (i+1,j), (i+1,j+1) gives the direction of the normal
for all triangles created from the quad.
* If * <
0 then the point is inside. If * >0
the point is outside. If *
n = 0, and if p is on the triangle then p=q and p in on the triangle.
* If *
= 0 and p is not on the triangle then p is outside.
One implication of this definition
is that the concept of shadows cast by open sheets no longer is valid.
Sheets may be considered to extend to the boundary of the geometry.
